Proefles Rekenen - Bestuderen
Vak: Rekenen
In deze les introduceren we de onder andere de volgende begrippen: breuken, tafel, redactie sommen, percentage en procent.
We introduceren ook een aantal oplossingsstrategieën voor breuksommen.
Met al deze kennis en informatie ben je in staat om bepaalde breuksommen te kunnen maken.
Lees de onderstaande informatie een aantal malen goed door en probeer de kernpunten goed te onthouden.
Klik op een hoofdstuk om de informatie te zien.
Eerst ga je op deze pagina kennis en informatie bestuderen.
Daarna ga je op de oefenpagina je vaardigheid in het gebruik van de kennis en informatie verhogen.
Tip: lees de informatie hardop voor (maar wel zo dat je anderen niet stoort).
Onderwerp: Breuken en Percentages Optellen en Vermenigvuldigen
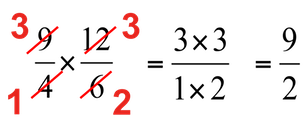
1. Breuken
Een breuk is een deel van een getal. Een breuk in het Engels heet een 'fraction'.
Breuken leren is belangrijk omdat je er elke dag mee te maken hebt.
Bijvoorbeeld om goed te kunnen plannen dat je niet teveel geld uit geeft, zodat je aan het einde van de maand nog geld over hebt.
Een breuk of gebroken getal is de onuitgewerkte deling van een geheel getal.
Bij een breuk zie je altijd een streep die breuklijn heet. Die streep kan horizontaal of diagonaal getekend zijn.
1/2 (een tweede), 1/3 (een derde) en 1/4 (en kwart) zijn voorbeelden van breuken.
Het getal boven de breuklijn is de teller. Het getal onder de breuklijn is de noemer.
In het Engels heet de teller nominator en heet de noemer denominator.
Breuken kun je optellen, aftrekken, delen en vermenigvuldigen.
1/4 + 1/3 + 1/2 = 13/12 = 1 1/12 = 1,08333333
Makkelijk Moeilijk Onbegrijpelijk
2. Tafels
Om goed te zijn in breuken moet je de tafels blijven oefenen. Elke dag weer. Van voor naar achter en van achter naar voren.
Hieronder staan enkele tafelsommen om je warm te draaien.
1 * 5 = 5
2 * 5 = 10
3 * 5 = 15
4 * 5 = 20
1 * 7 = 7
2 * 7 = 14
3 * 7 = 21
4 * 7 = 28
1 * 9 = 9
2 * 9 = 18
3 * 9 = 27
4 * 9 = 36
Etc...
Makkelijk Moeilijk Onbegrijpelijk
3. Kale Sommen
Een kale som is een breuksom met alleen maar getallen.
Voorbeeld 1: Hoeveel is 1/4 + 2/4? Antwoord: 3/4
Voorbeeld 2: Hoeveel is 8/25 + 8/25 + 9/25? Antwoord: 1 (25/25)
Makkelijk Moeilijk Onbegrijpelijk
4. Redactiesommen
Een redactiesom is een breuksom met een verhaaltje.
Voorbeeld 1: Mary heeft twee flesjes met water. De een is voor een kwart gevuld en de andere voor twee kwart. Hoeveel water heeft ze in totaal? En hoeveel heeft ze nog nodig om in totaal 1 fles water te hebben?
Het antwoord is: Ze heeft in totaal 1/4 + 2/4 = 3/4 (drie kwart) gevulde fles aan water. Ze heeft nog 1/4 (een kwart) nodig om in totaal een geheel gevulde fles aan water te hebben.
Voorbeeld 2: John heeft 25 mango's en 3 manden. In de 3 maanden wil hij zoveel mogelijk hetzelfde aantal mango's doen.
John verdeelt de mango's als volgt: 8/25 + 8/25 + 9/25 = 25/25.
Makkelijk Moeilijk Onbegrijpelijk
5. Gelijknamig maken
Wanneer we breuken gaan optellen wordt het optellen eenvoudiger als we ze gelijknamig gaan maken.
Dit noemen we een oplossingsstrategie. Zo zijn er nog veel meer oplossingsstrategieën.
Gelijknamig maken betekent dat je de delen van de breuk even groot maakt. De noemers van de breuk zijn dan gelijk.
Voorbeeld 1: 1/3 + 2/4 = 4/12 + 6/12 = 10/12
Voorbeeld 2: 1/7 + 2/8 = 8/56 + 14/56 = 22/56
Makkelijk Moeilijk Onbegrijpelijk
6. Vereenvoudigen
Vereenvoudigen is het minder ingewikkeld, gemakkelijker maken van een breuk. Dit doen we bij een breuk door de teller en noemer door hun grootste gemene deler te delen.
Voorbeeld 1: 3/6 + 7/14 = 1/2 + 1/2 = 1
Voorbeeld 2: 3/6 x 4/8 = 1/2 x 1/2 = 1x1 / 2x4 = 2/12 = 1/6
Voorbeeld 3: 9/4 x 12/6 = 3/1 x 3/2 = 3x3 / 1x2 = 9/2
Makkelijk Moeilijk Onbegrijpelijk
7. Breuken optellen
Breuken optellen doe je door eerst de breuken, voor zover mogelijk, te vereenvoudigen en daarna ze gelijknamig te maken.
Voorbeeld 1: 1/2 + 1/2 = 1
Voorbeeld 2: 1/3 + 1/4 = 4/12 + 3/12 = 7/12
Voorbeeld 3: 5/5 + 1/5 = 1 1/5
Voorbeeld 4: 2/4 + 3/6 = 1/2 + 1/2 = 1
Voorbeeld 5: 3/4 + 2/6 = 9/12 + 4/12 = 13/12 = 1 1/12
Makkelijk Moeilijk Onbegrijpelijk
8. Breuken vermenigvuldigen
Breuken vermenigvuldigen doe je door de tellers te vermenigvuldigen en de noemers te vermenigvuldigen.
Voorbeeld 1: 1/2 * 1/2 = (1*1) /( 2*2) = 1/4
Voorbeeld 2: 2/3 * 2/3 = (2*2) /( 3*3) = 4/9
Voorbeeld 3: 3/4 * 5/8 = (3*5) /( 4*8) = 15/32
Voorbeeld 4: 3/6 x 4/8 = 1/2 x 1/2 = 1x1 / 2x4 = 2/12 = 1/6
Voorbeeld 5: 9/4 x 12/6 = 3/1 x 3/2 = 3x3 / 1x2 = 9/2
Makkelijk Moeilijk Onbegrijpelijk
9. Percentages en Procenten
Een percentage is een gedeelte van een getal en wordt weergegeven met %.
1 procent is het honderdste gedeelte van een getal.
Voorbeeld: 1% van 100 is 1. 5% van 100 is 5.
Breuken en procenten geven allebei een deel van een geheel aan.
Bij elke breuk hoort een percentage en bij elk percentage een breuk.
1/100 deel = 1 %
Andere voorbeelden:
1/4 deel = 25 %
1/2 deel = 50 %
3/4 deel = 75 %
1 geheel = 100 %
Procenten zijn in feite breuken: 1% = 1/100. 5% = 5/100
Je kunt een percentage van iets berekenen door het met de bijbehorende breuk te vermenigvuldigen.
Voorbeeld: 50% van 40 = 40 × 1/2 = 20
50 % van 40 = 40 × 50 × 1/100 ( = 20)
Kernpunten
Kernpunten om goed te onthouden zijn:
- Maak breuken gelijknaming
- Vereenvoudig breuken
- Breuken in het Engels heten fractions
- Delen door een breuk is vermenigvuldigen met het omgekeerde
- 1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 6/12
- 2 * 5 = 10, 2/10 = 1/5
- 4 * 3 = 12, 4/12 = 1/3
- 6 * 9 = 54, 6/54 = 1/9
- 7 * 8 = 56, 7/56 = 1/8
- 3/4 deel = 75 %
- 1 procent is het honderdste gedeelte van een getal
- Bij elke breuk hoort een percentage
- Bij elk percentage hoort een breuk
Makkelijk Moeilijk Onbegrijpelijk
Volgende stap
Wanneer je de bovenstaande informatie een paar keer hebt doorgenomen, ga dan de oefeningen maken die hierbij horen.
Oefenen